Update: MOLUSCE is now available for QGIS 3.x. Check MOLUSCE page.
Together with Asia Air Survey we’ve developed MOLUSCE (Modules for Land Use Change Simulations) – a new tool based on QGIS that allows to perform quick and convenient analysis of land cover changes.
A researcher who analyses changes in landscape through time often deals with questions like:
- What are the changes and where did they happen?
- Which factors can explain the changes and strong is their explanatory power?
- What changes are expected in future and where?
The answer for the first question can be obtained by visual estimation, but to answer other questions one will need to set hypothises, verify them, derive conclusions and see how they meet the reality.
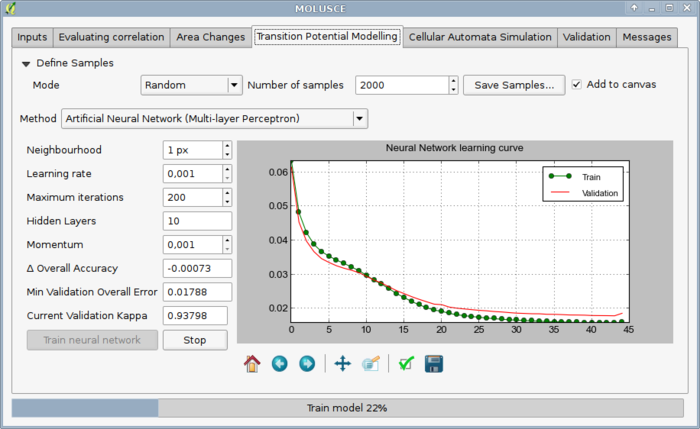
MOLUSCE is a toolbox to partially automate the process of answering such questions.
Briefly, the workflow consists of the following steps:
- Obtain landcover map for few time slices and a set of potential explanatory variables;
- Calculate probabilities of transitions from class to class;
- Build a model using ANN, logistic regression, Weights of evidence or Multi-criteria evaluation to describe transitions based on factor variables;
- Use this model for forecasting;
- Validate the result with real data.
Find more information in GIS-Lab article (Russian, autotranslated).

125 Responses to MOLUSCE – quick and convenient analysis of land cover changes